# Kratki osvrt na funkcije
|
|
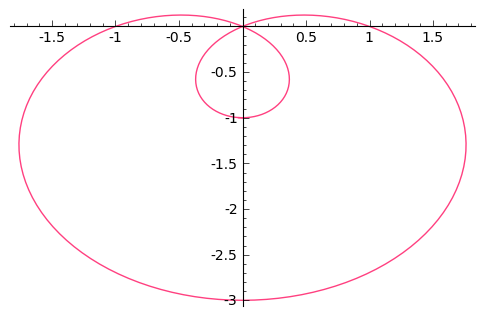
def f(k): L = [[sin(pi*i/100)+sin(pi*i/50),-(1+cos(pi*i/100)+cos(pi*i/50))] for i in range(-k,k)]; p = line(L, rgbcolor=(1,1/4,1/2)); show(p); return # k=90, 100, 101
|
|
f(101)
|
|
f = lambda x: x^2
f(4)
16 |
type(f)
<type 'function'> |
plot(f(x),x,-1,1, fill=true, fillalpha=0.1, figsize=[3,3], legend_label="f(x)", rgbcolor=(1,0,1))
|
|
def f1(x): return x^2
|
|
f2 = lambda x: x
|
|
f = Piecewise([[(-2,2),f1],[(2,4),f2]]);
|
|
f.plot()
|
|
A=matrix([[0,0,0],[0,0,0],[0,0,0]])
|
|
A.kernel()
Free module of degree 3 and rank 3 over Integer Ring Echelon basis matrix: [1 0 0] [0 1 0] [0 0 1] |
# Elementarna teorija brojeva - nekoliko korisnih naredbi
|
|
sum(divisors(15))
24 |
list(primes(1,29))
[2, 3, 5, 7, 11, 13, 17, 19, 23] |
next_prime(7)
11 |
26 in Primes(); 29 in Primes()
False True |
r=Integers(4)
|
|
r
Ring of integers modulo 4 |
a=r(2*3); a
2 |
x=r(3); y=r(6); x+y
1 |
M=MatrixSpace(r,3,3)
|
|
M
Full MatrixSpace of 3 by 3 dense matrices over Ring of integers modulo 4 |
M(0); M(1); M(2)
[0 0 0] [0 0 0] [0 0 0] [1 0 0] [0 1 0] [0 0 1] [2 0 0] [0 2 0] [0 0 2] |
A=M([[1,2,8],[2,3,1],[1,0,2]])
|
|
A*A # A^2
[1 0 2] [1 1 1] [3 2 0] |
p=Permutations(3)
|
|
p.list()
[[1, 2, 3], [1, 3, 2], [2, 1, 3], [2, 3, 1], [3, 1, 2], [3, 2, 1]] |
DyckWords(3).list()
[[1, 0, 1, 0, 1, 0], [1, 0, 1, 1, 0, 0], [1, 1, 0, 0, 1, 0], [1, 1, 0, 1, 0, 0], [1, 1, 1, 0, 0, 0]] |
q=Partitions(4)
|
|
for j in q: print j
[4] [3, 1] [2, 2] [2, 1, 1] [1, 1, 1, 1] |
a=Words("01") ; b=iter(a);
for i in range(8): print b.next()
word: word: 0 word: 1 word: 00 word: 01 word: 10 word: 11 word: 000 |
# Grafovi
|
|
D = DiGraph( { 0: [1], 1: [2], 2: [0]} ); D.show() # D.plot()
|
|
print D.edges()
[(0, 1, None), (1, 2, None), (2, 0, None)] |
import networkx;
K = networkx.complete_graph(3);
K.adj
{0: {1: {}, 2: {}}, 1: {0: {}, 2: {}}, 2: {0: {}, 1: {}}}
|
print K.edges()
print K.nodes()
[(0, 1), (0, 2), (1, 2)] [0, 1, 2] |

.png)
.png)
.png)